はじめに

今日は単回帰分析について解説するんだぜ!単回帰分析を使用すると、2つの変数の関係性を分析することができるんだぜ!

教えて、鹿!

ゆっくりしていってね!
例題
例えば、以下のような数学のテストと理科の点数の表があったとします。
| 数学 | 理科 | |
| Aさん | 80 | 90 |
| Bさん | 70 | 68 |
| Cさん | 40 | 55 |
| Dさん | 30 | 48 |
| Eさん | 30 | 39 |

ここで、以下の2つのことをやってみよう。
①数学の点数と理科の点数の散布図を描く。
②数学の点数と理科の点数の関係性を「良い感じ」に表した直線を引く(今のところは直感的に引けば大丈夫)。
皆さんも手を動かしてやってみてください。
単回帰分析とは?

こうかな?
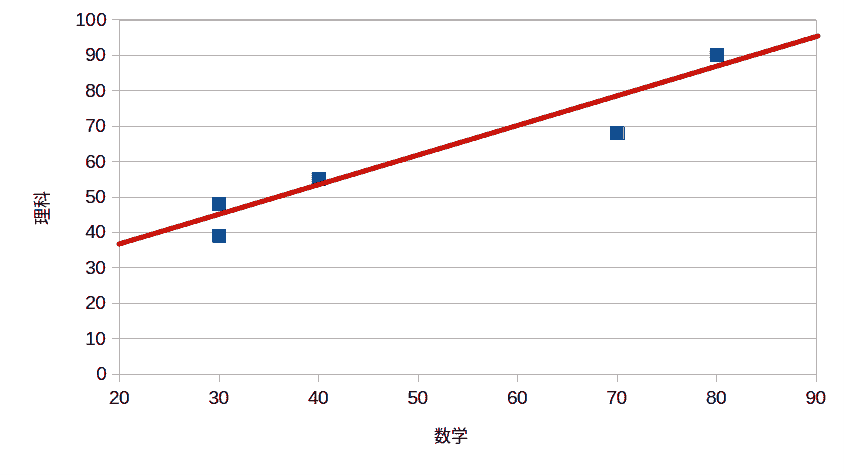

よくできたね。ここでは直感的に直線を引いてもらったけど、単回帰分析ではきちんと数学的に計算して、最も「良い感じ」な直線を引くよ。
「誤差(残差)」について
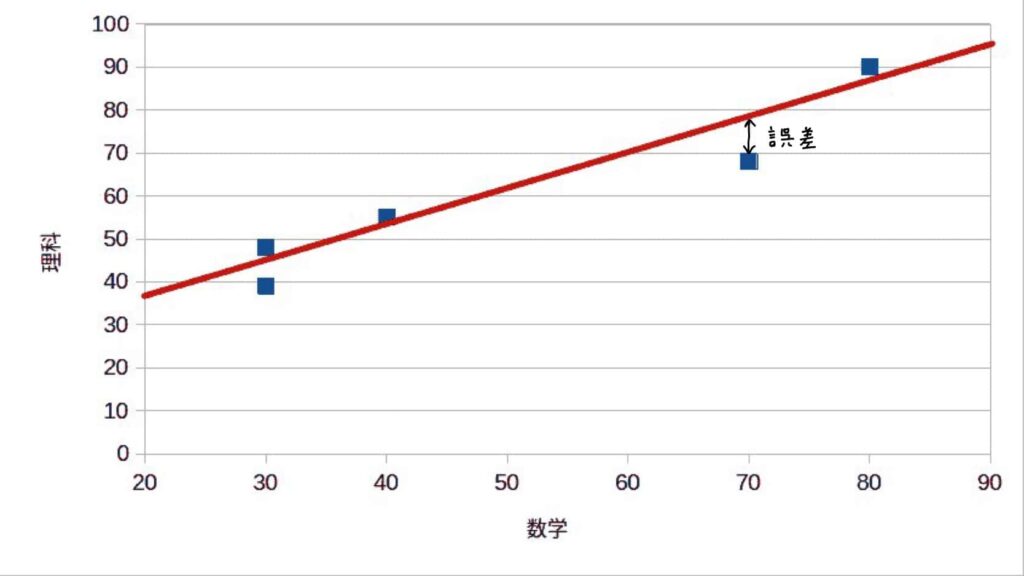
上記の図のように、単回帰直線によって求めた理科の点数と実際の理科の点数の差を「誤差」(あるいは「残差」)といいます。誤差にはプラスとマイナスがあり、実際の値が単回帰直線よりも上にあれば誤差はプラスで、実際の値が単回帰直線にりも下にあれば誤差はマイナスです。もちろん、単回帰直線と実際の値が重なれば誤差は0です。

誤差の絶対値は、大きいか小さいかだと、どっちのほうが良いかな?

そりゃあ、小さいほうがいいっしょ!

そうだね。
「どっちの直線のほうが良いかな?」クイズ

ここで問題。数学の点数をx、理科の点数をyとしたとき、2つの直線
・y = 1.2x
・y = 1.1x + 5
だったら、どっちのほうがより良い直線だといえるかな?

ええ…どうやればいいんだろう。

まずは、それぞれの直線で誤差を計算してみよう。
誤差を計算すると、以下のようになります。
| y = 1.2x | y = 1.1x + 5 | |
| Aさん | 6 | -3 |
| Bさん | -16 | -14 |
| Cさん | 7 | 6 |
| Dさん | 12 | 10 |
| Eさん | 3 | 1 |

5人全員、y = 1.1x + 5のほうが誤差の絶対値が小さくなった!こっちのほうが良い直線だ!

そうだね。でも、実際のデータ分析ではこんなに都合よくはいかないから、「誤差の2乗の合計」がより小さいほうが良い直線だとみなすよ。

なんで誤差を2乗するの?

それはまた別の機会に。
最も「良い感じ」な直線の求め方

ここでは2つの直線を比較したけど、実際には直線の引き方は無限にあるから、いちいち比較するわけにはいかないね。

たしかに…じゃあどうしたらいいの?

誤差の2乗の合計を最小化するような直線を計算するよ。

最小化…また難しいことをやりそうな予感…

最小化の方法まで理解しなくても、「誤差の2乗の合計を最小化するんだなー」っていうことを分かっていれば十分だよ。最小化は統計ソフトがやってくれるから

やったー!統計ソフトバンザイ!
次回予告
ここで紹介したのは、単回帰分析の最もメジャーで初心者向けの考え方ですが、次回はベクトルの考え方を使って単回帰分析を理解したいと思います。最初はとっつきにくいと感じるでしょうが、慣れれば単回帰分析や、その応用の重回帰分析、因子分析を直感的に理解できるようになります。