はじめに

今日は検定の基本、「t検定」について解説するよ!

わーい!何をするのか全然分かんないや!
なお、t検定には「対応のあるt検定」と「対応の無いt検定」がありますが、ここで紹介するのは基本となる「対応のあるt検定」です。
また、帰無仮説、標準化、確率分布の考え方についての理解があることを前提としています。不安な方は以下の記事を参考にしてください。
この記事はかなり分量が多くなるので、途中で休憩を入れながら読むことを推奨します。
例題
以下の例題のデータは、書籍『基礎から学ぶ統計学』(中原 治)から拝借しています。
コレステロール値を減らす効果があるかもしれないサプリがあるとします。サプリに本当に効果があるのかを調べるために、A, B, C, D, Eの5名の被験者にサプリを服用してもらい、服用前と服用後のコレステロール値を測定したところ、結果は以下のようになりました。
| 服用前 | 服用後 | |
| Aさん | 158 | 134 |
| Bさん | 148 | 135 |
| Cさん | 132 | 116 |
| Dさん | 107 | 110 |
| Eさん | 142 | 127 |
さて、このサプリは本当にコレステロール値を減らす効果があると言えるでしょうか?
t検定ってそもそも何をするの?

うーん、全然分かんないや

まずは、服用前と服用後のコレステロール値の差を計算してみよう。
以下の表は、服用後のコレステロール値から服用前のコレステロール値を引いたものとなります(つまり、値が小さいほどコレステロール値が減ったことになります)。
| 服用前と服用後の差 | |
| Aさん | -24 |
| Bさん | -13 |
| Cさん | -16 |
| Dさん | +3 |
| Eさん | -15 |

Dさんだけ少し増えてるけど、他の人たちはけっこう減ってる!これは効果あったんじゃないかな?

本当にそうかな?ただの偶然だったっていう可能性は考えた?

そこまでは考えてなかったや…
コレステロール値が増えたか減ったかでいえば、間違いなく減っているでしょう。これは表を見れば一目瞭然です。しかし、表を見ただけでは、この傾向がただの偶然かどうかを判断できません。

そこで、「検定」を行うことによって偶然かどうかを判断するよ。今回のようなケースだと、「対応のあるt検定」と呼ばれる手法が適切だね。

何をしようとしているのかまでは分かった!
まずは帰無仮説を立てよう

まずは帰無仮説を立てよう。帰無仮説は「AとBに差がない」という仮説だったね。今回はどんな帰無仮説が立てられるかな?

「サプリの服用前のコレステロール値とサプリの服用後のコレステロール値に差がない」かな?

だいたいそんな感じだね。より厳密には、「全人類がサプリを服用した場合の、服用前のコレステロール値の平均と、服用後のコレステロール値の平均に差がない」とすると良いよ。
なぜ「全人類がサプリを服用した場合の」としているかというと、答えは単純で、A, B, C, D, Eの5名のみに効果があるかではなく、他の人が服用しても効果があるかを推測したいからです。また、服用前と服用後のコレステロール値の平均値に差がないということは、前節の表の「服用前と服用後の差」を全人類で測定すると平均が0になるということです。これは重要なことなので覚えていてください。
母集団の標準偏差が分かっている場合の検定
今回実際にデータを得ることができたのはA, B, C, D, Eの5名だけです。この5名を仮に「グループ1」と呼ぶことにしましょう。しかし、t検定においては、「もしも5人グループを他にもいっぱい作ることができたらどうなるかな?」と考えます。
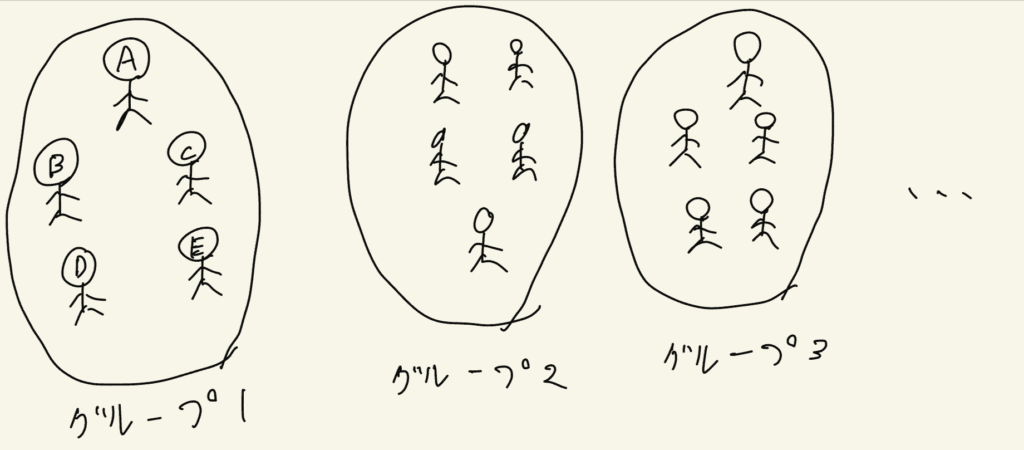

なんで?実際にはグループ1のデータしか無いのに?

そうだよ。今は理由が分からなくても大丈夫だよ。
ここで各グループの平均値(標本平均といいます)を表に記入すると以下のようになります。
| 標本平均 | |
| グループ1 | -13 |
| グループ2 | ? |
| グループ3 | ? |
| 以下略 |

ここで問題。標本平均の平均はいくらになるかな?

え?グループ1のデータしか無いんだから分からないよ

ここでは、「サプリの服用前と服用後のコレステロール値の差」を計算して、グループごとに平均をとっていることを思い出してみよう。そして、帰無仮説として、サプリを服用する前後でコレステロール値の平均値は変わらないことを仮定しているよ。

じゃあ…0かな?

正解!これは感覚的に理解したいところだね。
次に、標本平均の標準偏差を考えてみましょう。ただし、母集団(全人類)がサプリを服用した前後のコレステロール値の差の標準偏差は10であることが分かっているものとします。

なんで?5人にしかサプリを飲んでもらっていないのに、全人類がサプリを飲んだ場合の差分の標準偏差なんて分かるわけないよ

そうだね。だから実際の検定ではこれは推測するんだけど、まずは全体の流れを掴んでもらうために、こういう仮定をおいて話を単純にするよ。では、標本平均の標準偏差はどうなるかな?

さっきと同じ感じで考えて、10かな?

残念でした!10よりも小さくなるよ。
どうして標本平均の標準偏差は10よりも小さくなるのか?ひとことで言うなら、グループの平均をとることによって、個人間のばらつきがある程度相殺されるからです。例えば、中学校や高校で、クラスの中では成績の良い人と悪い人の差が目立っていても、クラスの平均点どうしを比べれば大した差は無かった、という経験は無いでしょうか?あれと同じ原理です。

具体的には、標本平均の標準偏差は、もとの分散をグループの人数の正の平方根で割ったものになるよ。つまり、今回なら\( 10 \div \sqrt{5} \)だね。

なるほど…
さて、ここで標本平均の平均と標準偏差が分かりました。そこで、グループ1の標本平均を標準化するといくらになるか考えてみましょう。標準化をすることによって、コレステロール値でも体重でも知能指数でも同じように分析できるからです。

標準化の方法は、「平均値で引いて、標準偏差で割る」だったね。

じゃあ\( (-13 – 0) \div (10 \div \sqrt{5}) \)かな?

正解!
グループ1の標本平均を標準化すると、\( \frac{-13}{10 \div \sqrt{5}}=-2.90688 \cdots \)となります。

ちなみに、標本平均を標準化したものは、「標準正規分布」という確率分布に従うんだ。標準正規分布では、-2.90688…という数は非常に珍しい値となるよ。
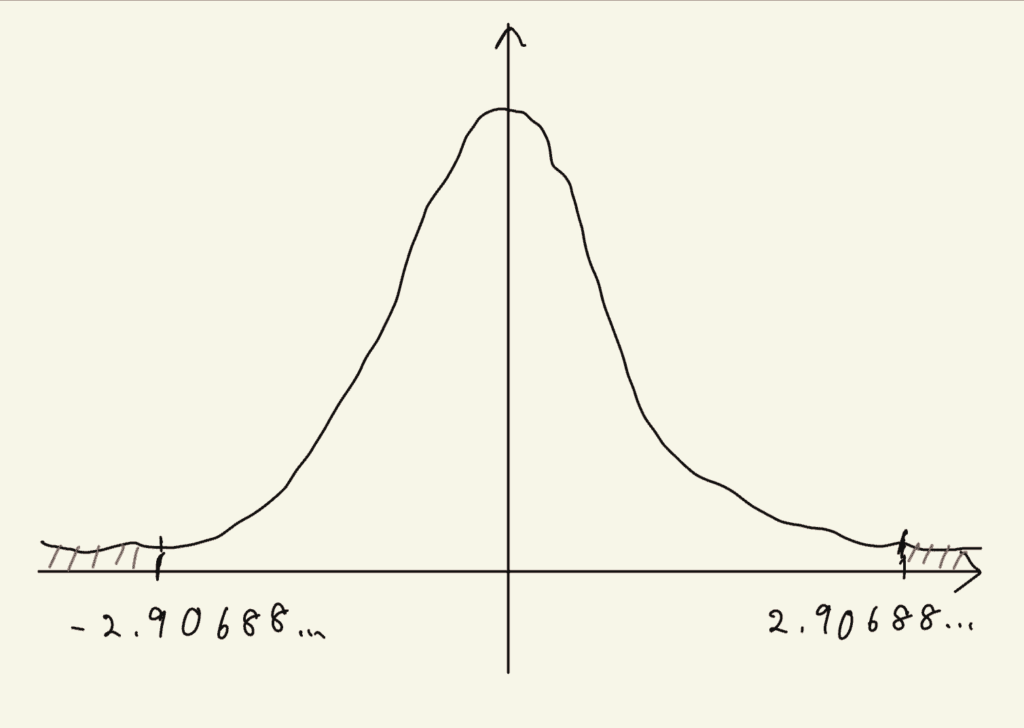
標本平均が-2.90688…よりも極端な値(より中心から遠い値)となる確率は、図の斜線の部分の確率になります(この確率をP値といいます)。図を見れば分かるとおり非常に低確率であり、5%にも満たない値となります。
つまり、帰無仮説が正しい(サプリに実は効果がない)と仮定すると、今回は確率にして5%にも満たないような偶然で、あたかもサプリに効果があるかのような結果が出てしまったことになります。しかし、確率は5%未満なので、統計的検定では「そのような偶然が本当に起こったとは考えにくい」と判断します。よって、帰無仮説が間違っていた(サプリには効果があった)と結論づけます。

以上が検定の流れだよ。ここまでお疲れ様!

疲れた…
母集団の標準偏差が分からない場合の検定

ここまでは、母集団の標準偏差が分かっていることを前提としていたね。でも実際にはたかしくんの言うとおり母集団の標準偏差なんか分かるわけないから、グループ1のデータから推測してみよう。

そうだった…

じゃあまずはグループ1のデータから分散を計算しよう!分散は偏差の2乗の平均だったよね!

そうなんだけど、母集団の分散を推測するときには偏差の2乗の合計を5で割ってはいけないんだ。代わりに1減らして4で割るよ。

なんで5じゃなくて4で割るの?

「自由度」という概念が関わってくるんだけど、難しいから「そういうものなんだな」と思ってもらえれば大丈夫だよ。
グループ1の偏差の平方和を4で割って分散を計算し、さらにその正の平方根である標準偏差を求めると9.87420…となります。先ほど使用した値である10とは少し異なる値が出ましたね。あとは、この標準偏差を使って前節と同じように計算していきましょう。

最後に1つ注意点。母集団の標準偏差を推測して検定を行う場合には、標準正規分布ではなく「t分布」という確率分布を使用するよ。標準正規分布と同じような形だけど、微妙に違う確率分布だよ。

疲れたー!

お疲れ様!
この記事はここで終わります。お疲れ様でした。