はじめに

今日は単回帰分析を、ベクトルの考え方を使って理解する方法を解説します。

あの、なんだろう、急に意味不明なこと言うのやめてもらっていいっすか?

最初は意味が分からないと思うけど、慣れると単回帰分析や、その応用の重回帰分析、因子分析を直感的に理解できるようになるよ。
データをベクトルで表してみよう①
例えば、こんなデータがあったとします。
| テストの点数 | |
| Aさん | 60 |
| Bさん | 50 |
| Cさん | 40 |

Aさん、Bさん、Cさんの点数を偏差に変換すると、どうなるかな?

10、0、-10っすね。

ここで、3人の点数のデータは(10, 0, -10)というベクトルで表すことができるよ。

ちょっと何言ってるのか分かんないっすね。
ベクトルの性質の復習

まずはベクトルの復習をしよう。ベクトルは「向き」と「大きさ」の2つをもつものだったね。

そんなことを高校でならった気がするね。

では2つ問題を出そう。
① (1,2,3)というベクトルを、大きさはそのままにして向きを反対にするとどうなる?
② (1,2,3)というベクトルを、向きはそのままにして大きさを2倍にするとどうなる?

向きを反対にすると(-1, -2, -3)で、大きさを2倍にすると(2,4,6)かな?

そうだね。
ベクトルの概念を思い出してきたら、次に進みましょう。
データをベクトルで表してみよう②

3人のテストの点数をベクトルに変換した(10, 0, -10)にも当然向きと大きさがある。問題は、それが何を表しているかだね。

何を表しているの?

向きは「傾向」、大きさは「傾向の強さ」だと考えればいいよ。

ほ、ほう…
なお、ここで言う「傾向」というのは、平均値を基準として、誰の点数がどれくらい高くて、誰の点数がどれくらい低いか、的なものだと考えてください。

例えば、このベクトルの大きさはそのままに、向きを反対にするとどうなるかな?

(-10, 0, 10)だね。

つまりAさん、Bさん、Cさんの点数の偏差が順に-10, 0, 10になったことになる。傾向がちょうど逆転したのが分かるかな?
次は向きはそのままに、(10, 0, -10)の大きさを2倍にするとどうなるかを考えてみよう。

(20, 0, -20)だね。

つまりAさん、Bさん、Cさんの点数の偏差が順に20, 0, -20になったわけだね。傾向がより強くなったのが分かるよね。
どうでしょうか?データをベクトルで表す感覚に慣れてきましたか?
単回帰分析のベクトル的表現

では、今度は単回帰分析をベクトルで表現してみよう。
ここでは、理科のテストの得点を、数学のテストの得点から予測することにします。ここで、理科のテストの得点をベクトルに変換したものをy、数学のテストの得点をベクトルに変換したものをxとします。また、yの予測値の偏差をベクトルに変換したものを\( \hat{y} \)とし、誤差をベクトルに変換したものをeとします。
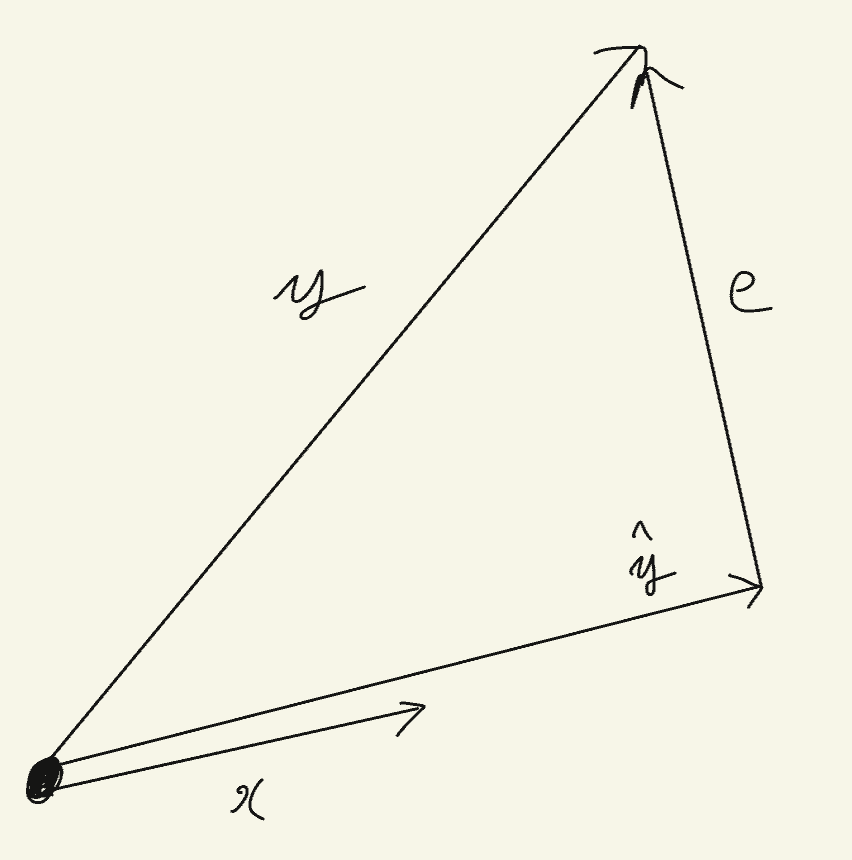

まず、\( \hat{y} \)はxと同じ、または反対の向きになる。

なんで?

単回帰分析では、「xの値が大きいほどyの値も大きい」、または「xの値が大きいほどyの値は小さい」という予測をするからだよ。だから、予測値のベクトルである\( \hat{y} \)はxのベクトルと向きが同じか反対になるよ。

ほーん

次に誤差のベクトルeについて。誤差はy – \( \hat{y} \)で求められるから、\( \hat{y} \)の終点とyの終点をつないで図のようになるね。

誤差も偏差に変換してあるの?

誤差は偏差に変換していないよ。
それから、yベクトルを\( \hat{y} \)とeベクトルに分解できる点にも注意しよう。これはつまり、yベクトルを「xで予測できた部分」と「xで予測できなかった部分」に分解しているといえるよ。
誤差ベクトルの大きさの最小化と分散説明率

ここで、eベクトルは誤差なんだから小さいほうが良いよね。eベクトルの大きさを最小化するとき、\( \hat{y} \)ベクトルとeベクトルのなす角度はどうなるかな?

えっと、、、直角かな?

そうだね。だから、\( \hat{y} \)とeが直角になるようなときに\( \hat{y} \)は最適になるよ。
余裕のある人向けに、単回帰分析の予測の正確さを表す「分散説明率」について説明します。
\( \hat{y} \)とeが直角になるということは、\( \hat{y} \)とeとyによって形成される三角形は直角三角形となります。よって、三平方の定理により、以下の定理が導けます。
(yベクトルの大きさの2乗) = (\( \hat{y} \)ベクトルの大きさの2乗) + (eベクトルの大きさの2乗)
この数式は何を表しているのでしょうか?あえて日本語で表すなら、「yの分布の散らばりを、xによって説明できる部分とxによって説明できない部分に分解した」といったところでしょう。
そして、「では、yの分布の散らばりのうち、どの程度がxによって説明されたのか?」を表すための概念として「分散説明率」があります。求め方は簡単で、
(\( \hat{y} \)ベクトルの大きさの2乗) ÷ (yベクトルの大きさの2乗)
です。これが大きいほど、yはxによって正確に予測されたことになります。
最後に

単回帰分析がベクトルで表せるのは分かったけど、なんでわざわざこんな変な方法を使う必要があるの?

たしかに、単回帰分析ならベクトルを使わない方法でも簡単に理解できるね。でも、もっと発展的な内容である重回帰分析や因子分析、さらには偏回帰分析などを理解するにあたっては、このベクトルの考え方を使ったほうが理解しやすいんだ。だから、最初はとっつきにくくても、ベクトルを使った考え方に慣れておくことをおすすめするよ。
残念ながら、本記事執筆時点では、ベクトルの考え方を使って重回帰分析などを理解する方法については記事を書けていません。興味のある方は、https://amzn.asia/d/gIND7rcを参照してください。