結論
確率密度は、「確率の密度」としか言いようのないもの。確率分布は確率密度のグラフで、正規分布は現実世界でよくある確率分布のパターン。
はじめに

「確率の密度」って何?いきなり全然わからないよー!

そうだね。でも確率分布は本当に言葉で表現しにくい概念なんだ。でも大丈夫、これから具体的な例を交えて説明していくよ。
なお、以下の説明では、微分・積分についての基本的な知識があることを前提としています。
問題1
変数xは、-1から1の間の数値をランダムにとります。どのくらいの値が出やすいとか、そういったことは一切無いものとします。ここで、関数P(a) を以下のように定義します。
P(a) = 「x < a」となる確率(ただしaは実数)
では、P(a)のグラフを描いてみましょう。

これなら描けそうな気がするぞ!
問題1の答え

これでどうかな?
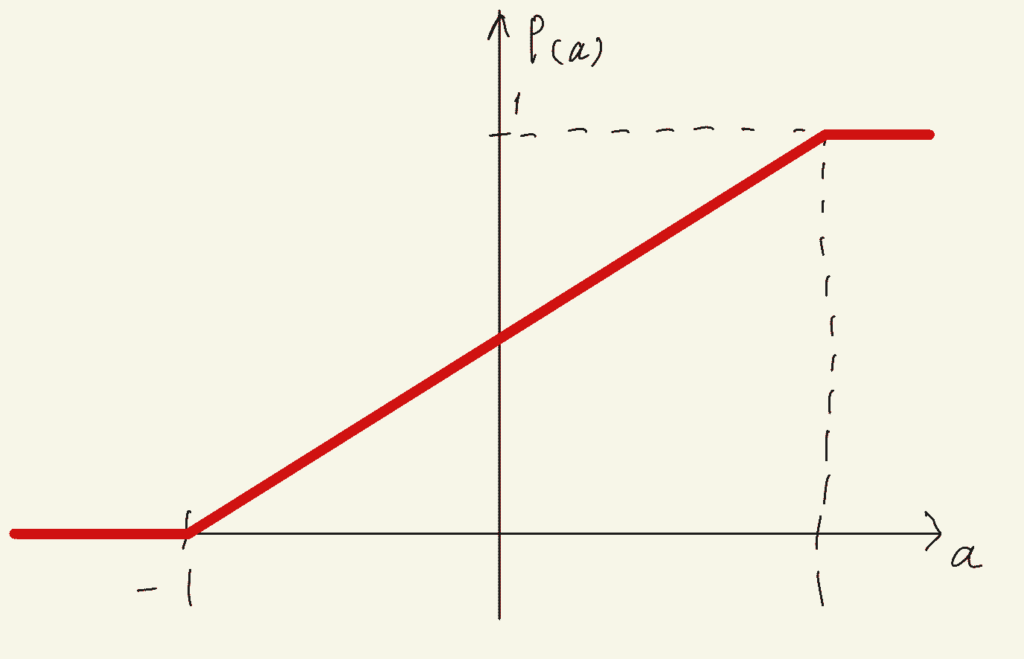

正解!よくできたね。
グラフが汚いのはお許しください。このグラフを見ると、aが-1以下のときはP(a) = 0で、aが1を超えるとP(a) = 1になるのが分かると思います。また、aが0のときはP(a)は「x < 0」になる確率なので、確率はちょうど0.5です。
問題2
今度は、P(a)を微分したP'(a)のグラフを描いてみましょう。

微分ってなんだったっけ?

微分は、グラフの傾きを求めることだね。

高校でそんなことを習ったっけ。P(a)のグラフは形が単純だから、微分も簡単そうだね!
問題2の答え
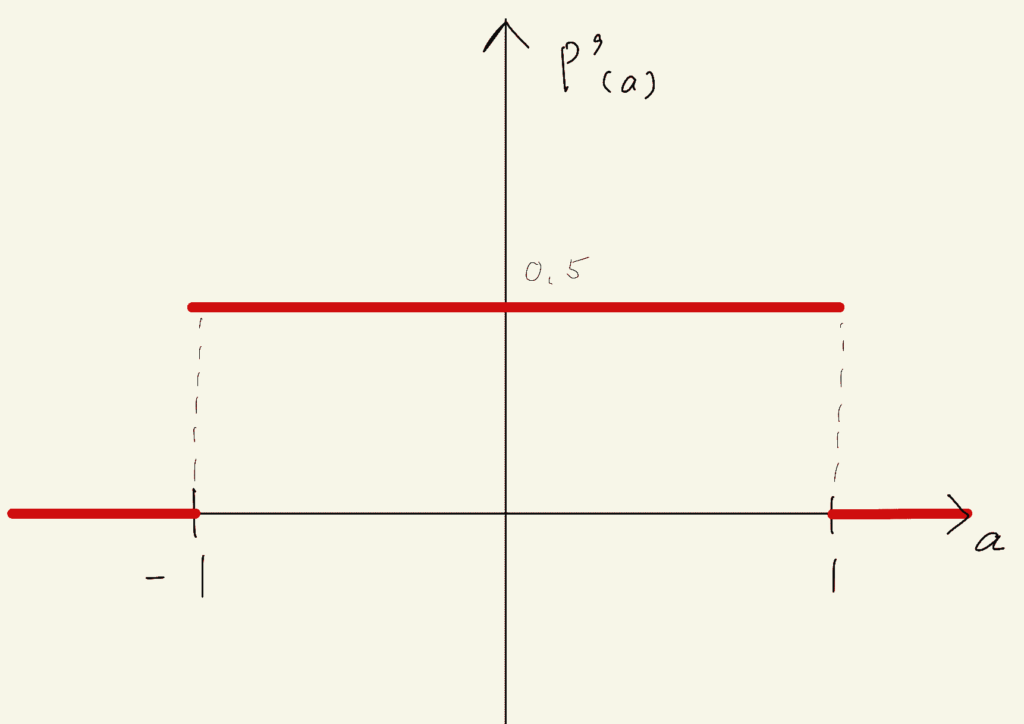
シンプルなグラフができました。皆さんはできましたか?

描けたぞ!

よくやったね。実は、これが変数xの確率密度のグラフなんだ。

え、これが?なんだか分かったようで分からないような…
鹿の言うとおり、これはxの確率密度のグラフ(つまり確率分布)です。-1 < a < 1の範囲ではP(a)は一定のペースで増加するため、その区間において確率密度P'(a)はずっと0.5という一定の値になります。確率密度が「確率の密度」だということが少し分かってきたのではないでしょうか?
確率密度を積分してみよう

さて。では、今度は確率密度を積分してみよう。

今度は積分???

そう。-1から0の範囲で積分してみよう。
皆さんもちょっと手を動かして、計算してみてください。

積分したら0.5になったぞ!
P'(a)を-1 < a < 0の範囲で積分するわけですから、P(0) – P(-1)を計算すれば良いですね。分からなかった人は先に積分の復習をしてから再度挑戦してみましょう。

ところで、P'(a)を-1から0の範囲で積分したものには、2つの意味があるんだ。
①「〇〇の面積」
②「-1 < a <0の範囲でのP(a)の〇〇」
〇〇の中に入る言葉が分かるかな?

分かった!
①「P'(a)のグラフの-1 < a < 0の部分の面積」
②「-1 < a < 0の範囲でのP(a)の増加量」
だ!

そうだね。じゃあ、②の「 -1 < a < 0の範囲でのP(a)の増加量」は何を表しているかな?

-1 < x < 0になる確率かな?

正解!
このような理由から、例えば確率分布の-1 < a < 0の部分の面積は、-1 < x < 0になる確率と一致します。これは非常に重要なことなので、必ず覚えていてください。
問題3. もう少し複雑な確率分布

ここまでは、xは-1から1の間の数を完全ランダムにとるという前提だったね。今度は、次のように条件を変えて考えてみよう。
「xはすべての実数をランダムにとる。ただし、0に近い値ほど、とる確率が高い。」
P(a)とP'(a)のグラフはどうなるかな?

急に難しくなってきた…
皆さんは分かるでしょうか?たかしくんと一緒に考えてみましょう。
問題3の答え

これでどうかな?
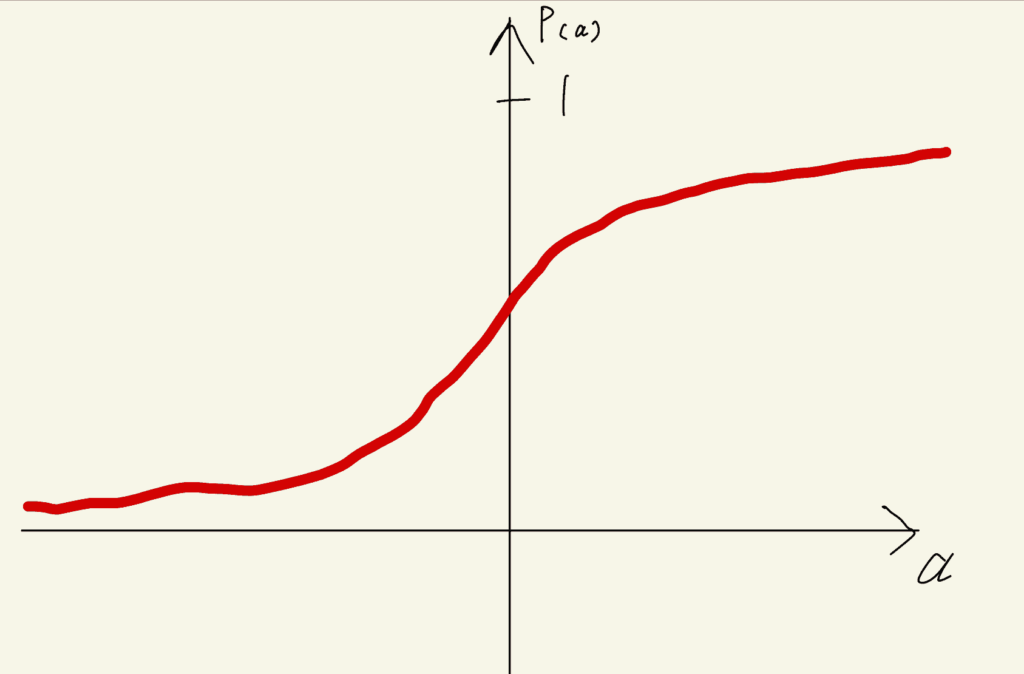
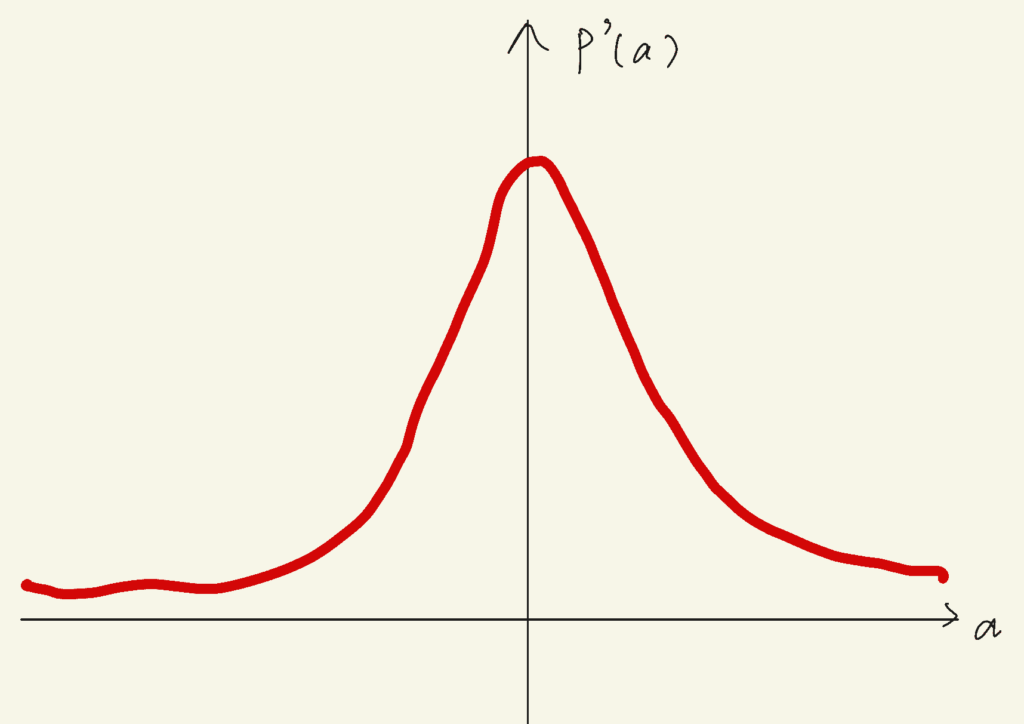

よくできたね!
不思議な形のグラフができました。なお、「0に近い値ほど出やすい」という曖昧な条件設定だったので、厳密な正解はありません。だいたいこういう感じの形になっていればOKです。
現実の世界において多いのは、問題2のようなシンプルな確率分布ではなく、問題3のようなやや複雑な確率分布になります。アンケートの回答やテストの得点など、たいていのものは平均値や中央値に近い値ほど出やすいからです。

統計でよく使うのが「正規分布」という確率分布だよ。これは現実の世界においてよくある確率分布の形で、ちょうど上記のP'(a)のグラフのような山なりの形をしているよ。

確率分布が分かっていれば、正規分布は簡単だね!
まとめ
確率密度は、「確率の密度」としか言いようのないもの。確率分布は確率密度のグラフで、正規分布は現実世界でよくある確率分布のパターン。

あ、冒頭のコピペだ!でも、最初よりも何を言っているのか分かるようになった!


